前回の回帰分析に続いて今度は単純パーセプトロンやってみました。
昔は、C言語使ってたので行列計算の時はかなり苦労しましたが、
Numpyすごいですね。For文の数がとても減りました。
今回は、乱数で、
下記のような緑色のポイントと、青色のポイントを作って、
それらを分類する直線を単純パーセプトロンで求めました。
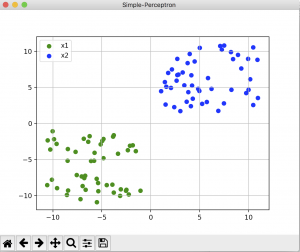
教師あり信号は、緑色を-1, 青色を+1として与えました。
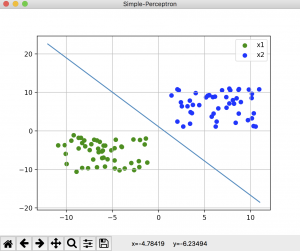
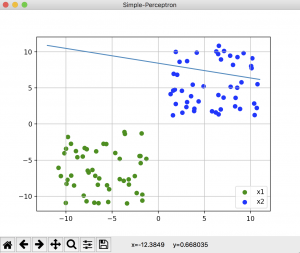
結果はこんな感じです。
うまくいった結果
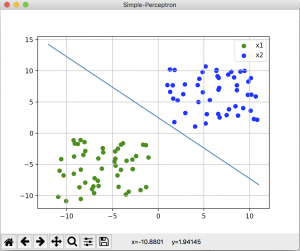
だめだった結果(学習たりてない)
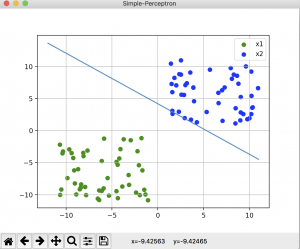
何回か繰り返しているとたまに、どこに向かってるのかよくわからないレベルの分類線が出てきますw
コードは下記です。
下記参考サイト1のコードをベースに、自分で理解をしながら書き換えていったものです。
(参考サイトの人ありがとうございました。勉強になりました。)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
# -*- coding: utf-8 import numpy as np import pylab as plt # 識別関数の本体:y=w'xを計算 def predict(wvec, xvec): out = np.dot(wvec, xvec) if out >= 0: res = 1 else: res = -1 return [res,out] # 学習部:識別関数に学習データを順繰りに入れて、重みベクトルを更新 def train(wvec, xvec, label): [res,out] = predict(wvec,xvec) c = 0.5 if out*label < 0: wtmp = wvec + c*label * xvec return wtmp else: return wvec if __name__=='__main__': TRAIN_NUM = 100 # 学習データは偶数個 TRAIN_NUM_H = int(TRAIN_NUM/2) LOOP=1000 # ループ回数 wvec=[1,-1,1] # 重みベクトルの初期値、適当 # 学習データは平面状の直行座標における、第1象限と第3象限に50個ずつ # t_data = [x1(横軸座標値), x2(縦軸座標値), z(バイアス項)] t_data = 10 *(np.random.rand(TRAIN_NUM,3)) +1 # 座標の半分は1~11の実数を乱数でセット。 t_data[0:TRAIN_NUM_H,:2] = -1 * t_data[0:TRAIN_NUM_H,:2] # 座標のもう半分は、x1とx2を-11~-1とする。 t_data[0:TRAIN_NUM , 2] = 1 # とりあえず1に固定。 # 教師ラベルを1 or -1で振る s_labels = np.ones(TRAIN_NUM) s_labels[TRAIN_NUM_H +1:TRAIN_NUM] = -1 # ループ回数の分だけ繰り返しつつ、重みベクトルを学習させる for j in range(LOOP): for i in range(TRAIN_NUM): wvec = train(wvec, t_data[i,:], s_labels[i]) # 分離直線を引く x_fig=range(-12,12) y_fig=[-(wvec[1]/wvec[0])*xi-(wvec[2]/wvec[1]) for xi in x_fig] # グラフ作成 plt.figure("Simple-Perceptron") # 分離対象と分離直線をグラフに表示 plt.scatter(t_data[0:50 ,0] , t_data[0:TRAIN_NUM_H, 1], color='g', label="x1") plt.scatter(t_data[51:TRAIN_NUM,0], t_data[51:TRAIN_NUM , 1], color='b', label="x2") plt.plot(x_fig,y_fig) plt.legend() plt.grid() plt.show() |
次からは、少しだけ、識別関数のランクをあげてみたり、
中間層1層のニューラルやっていきたいな。
参考サイト1:https://tjo.hatenablog.com/entry/2013/05/01/190247
参考サイト2:http://tkengo.github.io/blog/2016/06/03/yaruo-machine-learning4/